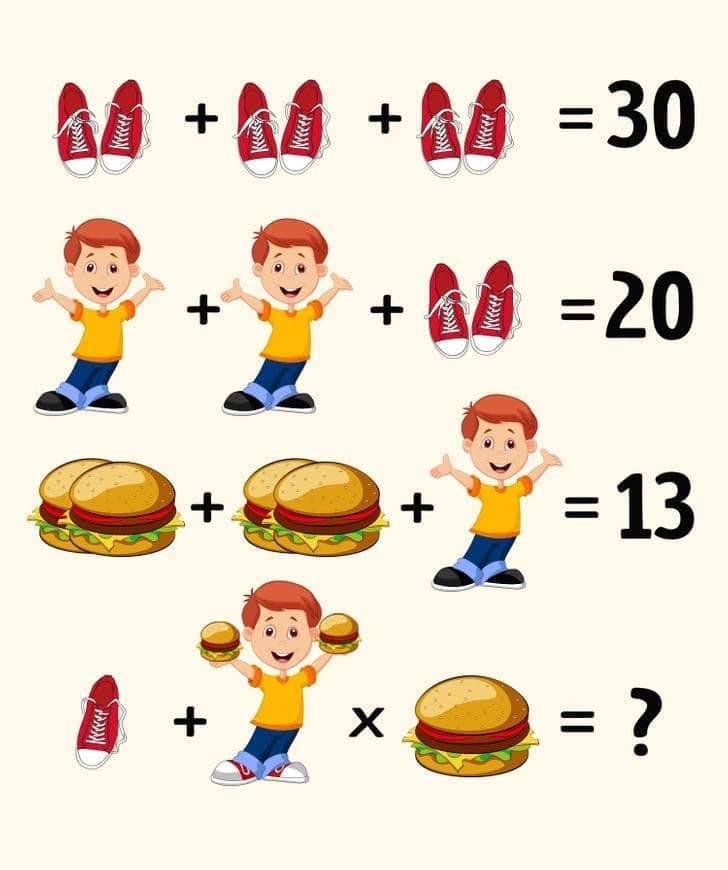Let’s solve this step by step:

First equation:

$$\text{Shoes}+\text{Shoes}+\text{Shoes}=30$$This implies each pair of shoes is $10$:

$$10+10+10=30$$Second equation:

$$\text{Boy}+\text{Boy}+\text{Shoes}=20$$Since the shoes are $10$, we have:

$$2\times \text{Boy}+10=20$$Solving for the boy:

$$2\times \text{Boy}=10\Rightarrow \text{Boy}=5$$Third equation:

$$\text{Burger}+\text{Burger}+\text{Boy}=13$$We know the boy is $5$, so:

$$2\times \text{Burger}+5=13$$Solving for the burger:

$$2\times \text{Burger}=8\Rightarrow \text{Burger}=4$$Final equation:

$$\text{Shoe}+(\text{Boy with two small burgers})\times \text{Burger}=?$$ A single shoe is half of a pair, so it’s $5$. The boy with two small burgers should represent $5+2=7$. The burger is $4$.Now, substitute into the equation:

$$5+(7\times 4)=5+28=33$$Answer: 33